So, if you're from a tech background or you've mistakenly tried to solve coding problems on platforms like LeetCode, CodeChef, etc. (actually, I only know these two, so you know, just using etc.), then you might have had an encounter with the above two terms.

And I'm damn sure that you may have initially ignored these two terms, but when things start to get worse, you wake up and think, 'I need to cover up this first.'

There are many talented and smart people (fewer in number) who will learn these concepts first and then tackle coding problems on platforms.

So, if you're from the above two categories (anyone can watch), then let's get started!

Time Complexity

Studied gravity? Then you must know that in a vacuum, an ant and an elephant will take the same time to fall from a height (consider it if you don't know). So, the time taken doesn't actually depend on the weight of the ant and elephant. Now, what does this time depend on? It depends on the height from which the two buddies are falling.

Now, the most important question arises: 'We're here to study time complexity, so why the heck am I telling you about gravity, ants, and elephants?' So, let's get to the main point.

If you take an old-time computer and a brand-new Mac, and then run a code on both machines, you might be surprised that the time taken on both machines is the same.

Actually, many people and so-called YouTubers teach that time complexity is the time taken, which is absolutely bullshit. In simpler words:

Time Complexity != Time Taken

What actually is Time Complexity !!

So then you might be asking "Hey if time taken is not time complexity then what is time complexity ?" , actually time complexity can be understood by the function which gives us relationship about how the time will grow as input grows. In simpler words if you increase the input in your program then how time will grow. Let me explain this with a graph :

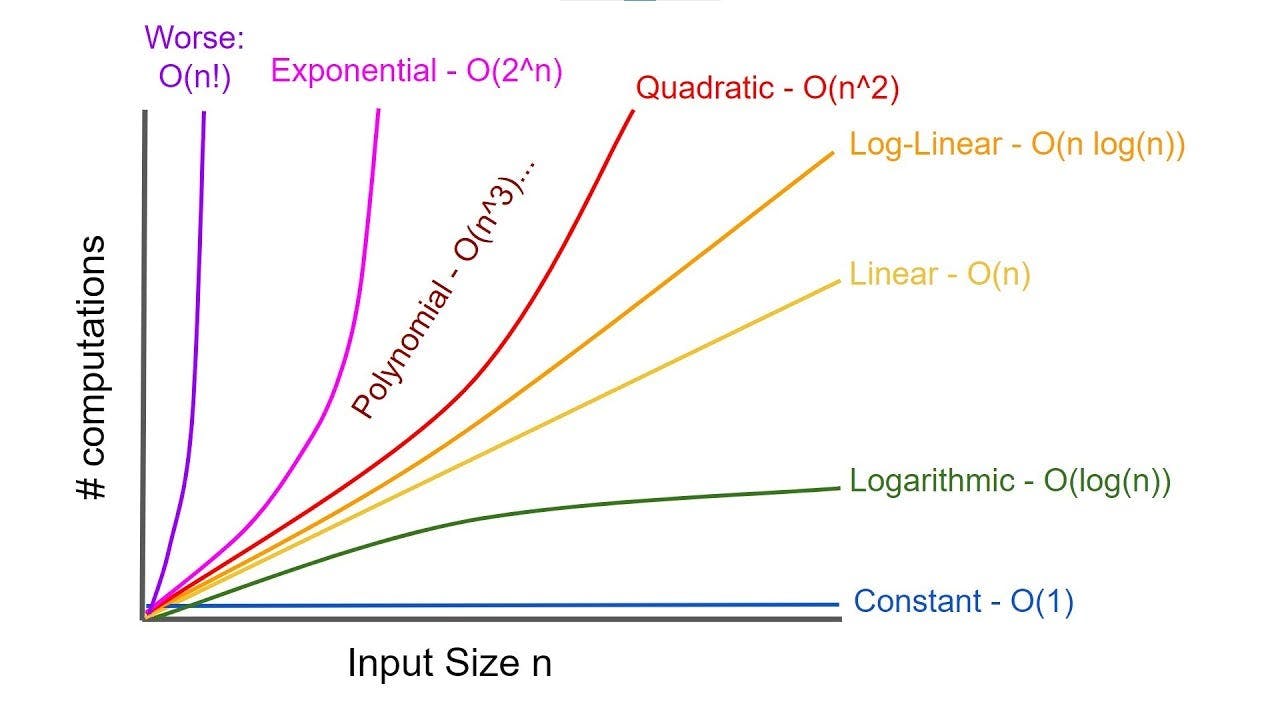
The graph is plotted between Time Taken with Input Size. From the graph, we can see that as the input size increases, different functions change, and we can conclude that:

O(1) < O(log-N) < O(N) < O(N log-N) < O(N^2) < O(N^3) < O(2^N) < O(N!)

So, from the graph, you can conclude that the worst case is the factorial function, which increases so rapidly with a slight increment in input.

Now, coming to the main point, everyone likes that their code must take less time, and for that, you must know what function you are dealing with and how the time will change with an increase in input size by the function. And as you all know, 'LESS TIME, GOOD CODE ; MORE TIME, JUST F*CK OFF. "

What to consider during time complexity

Now there are some simple steps which you can consider while thinking complexity.

1. Always look for the worst-case complexity and be sure that the approach you are trying or thinking to apply doesn't fall under the worst case.

2. Always look at the complexity of large or infinite data because there might be chances that the complexity which is good for small data might not be suitable for large data.

3. This one is tricky; actually, we don't care about actual time but care about how time is changing, i.e., the function. So ignore constants as they will not have any effect.

   Example : The functions y=2x, y=5x, y=10x, y=100x are all linear and that's the thing we need , nature of function , so don't worry if it has any type of constant.

4. Always ignore less dominating terms. Let me help you understand with an example.

   Example: Suppose you have data for 1 million people in an array, and it follows two complexities, i.e., N^3 and log-N. So the time complexity is O(N^3 + log⁡-N). We can ignore log-N in front of 1 million. Let me explain it in more detail:

   Put the value of N. We will get (1 million)^3+log(100000).

   This will give us ((1000000)^3+6). Now, I don't think that you will be considering 6 unless you have the responsibility for the success of the Apollo mission where these small values matter.

Now you might be wondering that what is O or why I'm using O, Actually it's called Big O notation. So there are basically five types of notaion and maybe you only need to have an idea of what it's saying, so these are :

Big O Notation

It's called the upper bound, and simply put, it means that if you are given a complexity, let's say O(N^3), then there are zero chances that the problem will be solved in higher complexity. However, it can be solved in less complexity, like O(N^2) or in O(N), but not with O(N^4).

Big Omega Notation

It's the opposite of Big O notation; it's lower bound. By lower bound, I mean that for N^3, the program needs at least N^3 complexity, and there are high chances that it will take even more complexity.

Now, what if I tell you that the actual, or we can say the real thing, is yet to come, and there are high chances that you will love the blog after completing time complexity.

So let's get started !!

Now you might be having that what is the use of this so called a very important topic Time Complexity, so let me first tell you importance and benefits of undertanding time complexity :

Suppose you are given 100 integers in an array and you want to sort the elemnts in ascending order then ther are two approaches :

1. You can do Bubble Sort of complexity of O(N^2).

2. You can also do Merge Sort of complexity O(Nlog(N)).

And there are plenty of examples by which you can understand how important is Time Complexity.

And now the question comes that we can find Time Complexity of simple problems but what about time complexity of a complex problem, then here is the solution :

1. Convert your problem into equation.

   Example : There is a concept in DSA called Binary Search which can be written as O(N/2) + O(1). (Don't worry if you don't know know as you'll be learning this later and also you'll be learn to covert problems into equations with time.)

2. Now you can apply several methods like "Plug and Chug", "Master's Theorem" which you may have learned in your college or might be learning.

3. Then finally tou will find your Time Complexity.

But wait a second, are you one of those who haven't studied the above methods (just like me 😅)? If so, I have something for you that I think you'll definitely love.

Akra-Bazzi (The Men-The Myth-The Legends)

So, there was an equation that many scientists attempted to solve but failed, ultimately concluding that the equation was already in its simplest form. One day, two students went to their college professor and confidently claimed they might have cracked the problem. To everyone's surprise, they indeed solved the problem that had stumped many scientists before.

Now, I feel I might not be the right person to explain the theorem, as Professor Mr. Tom Leighton, who approved the equation, has already created a video on MIT's official channel. Another YouTuber has also provided a clear explanation of the concept. It's up to you to decide from whom you want to study. I'm attaching the links to both videos (please watch, as I'm confident you'll enjoy the lecture).

After investing so much time and energy in understanding time complexity, let's now tackle Space Complexity!

Space Complexity

Now it's actually very straight topic and it simple means space used by algorithm to get executed and it also uses tha same Big O Notation as stated above.

Space Complexity = Input Space + Auxilary Space

Now Input Space is the amount of space that you are taking as an input in the problem.

Example : Suppose you are asked to take an array on n elements then Input space is O(N).

Auxiliary space is space which algorithm uses during execution.

Example : In Binary Search we have to take three variable to compare and assign so it uses O(3) which is constant.

So that's all about Time and Space Complexity, and I really hope that now you might have a better understanding of the terms compared to the knowledge you had before.